Unfair Coins and Bayes' Theorem
This post works through an example that I struggled with early on in learning Bayesian statistics. I think some of the notation below is nonstandard, but hopefully the ideas are clear.
One thing that’s a bit unclear in many popular presentations of Bayesian reasoning is how to apply it in some of the simplest cases. As an example, suppose we have a coin, and there’s a question of how fair it is. We can model this as a Bernoulli distribution, which has a parameter $p$. A fair coin would have $p={1 \over 2}$.
My intuitive prior is that it is a fair coin $p={1\over 2}$. I flip it 20 times, and discover that it landed heads 15 times. What do I do now?
It seems like this is evidence that the coin is not fair, but it’s not obvious where to plug this into the standard Bayes formula:
\[P(H|D) = {P(D | H) \cdot P(H) \over P(D)}\]Here $D$ is our data, that it came up heads 15 times. $H$ is, hrm, $p={1\over 2}$? So then we can compute the likelihood in the usual way:
\[P\left(D \; \middle | \; p=\frac{1}{2}\right)=p^{15} (1 - p)^5 {20 \choose 15} = \left({1 \over 2} \right)^{20} {20 \choose 15}\approx 0.015\]This suggests that the coin is probably not very fair, as you’d expect. But what are $P(H)$ and $P(D)$ in that formula?
The key point is that the prior wasn’t a rich enough structure to do the computation we want to do. We actually need to assign a credence for every value $p$ that goes into our model, and we need to make that precise. This means we need a probability distribution $B_0$ with domain $[0, 1]$, i.e. $B_0: [0, 1] \to \mathbb{R}_{\geq 0}$ with $\int_0^1 B_0(p)dp =1$.
At that point, we can compute $P(D)=\int_0^1 B_0(p)\cdot {20 \choose 15} \cdot p^{15} \cdot (1-p)^5 dp $, and other pieces fall into place.
A simple way to express a prior this might be that I examined the coin, and it feels like an ordinary coin. That suggests that if it’s not fair, it’s probably not too unfair, so we could make the prior “it could be anything between $p=0.4$ and $p=0.6$, with other values being basically impossible. This lets us define a prior piecewise as:
\[B_c(p) = \begin{cases} 0 & 0\leq p < 0.4 \\ 5 & 0.4\leq p\leq 0.6 \\ 0 & p> 0.6 \end{cases}\]Then we can compute $P(\textrm{heads}=N)$ relative to this prior, e.g. using sympy:
import sympy
from sympy import *
from IPython.display import display
p, N = symbols("p N")
B_c = Piecewise((0, p < 0.4), (0, p > 0.6), (5, True))
likelihood_D = sympy.binomial(20, 15) * p** 15 * (1-p)**5
P_D = integrate(B_c * likelihood_D, (p, 0, 1))
display(P_D)
$\displaystyle 0.0225965086622404$
Furthermore, the output of a Bayesian update isn’t a single number, it’s another distribution that’s based on both our prior distribution and the data. Let’s call the posterior distribution $B_D(x)$. It’s given by Bayes’ formula, as you’d hope:
\[B_D(x) = \frac{P(D|p=x)\cdot B_c(x)}{P(D)}\]As you’d hope, if we integrate it on $[0,1]$, we get $1$. This is checked numerically below, though you can also check this yourself by noting that $P(D)$ is a constant, and pulling it out of the integral.
Numerical check:
integrate(likelihood_D * B_c / P_D, (p, 0, 1))
$\displaystyle 0.999999999999983$
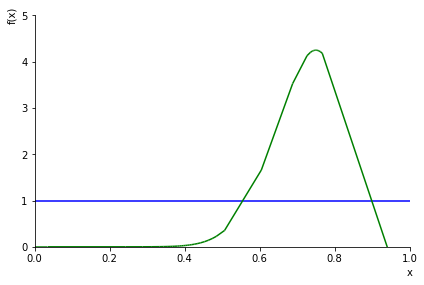
We can graph the prior (blue) and the posterior (green) distributions to get a feel for what the update looks like:
%matplotlib inline
p1 = plot(B_c, xlim=[0,1], show=False, line_color='b')
p2 = plot(likelihood_D * B_c / P_D, show=False, line_color='g')
p1.append(p2[0])
p1.show()
The shape of the graph indicates that we assign a much higher credence to the coin favoring heads than before. But we also assign a probability of $0$ to the value that seems to match the data best $p={15\over 20}$. Is that correct? Generally speaking, we don’t want to assign a probability of literally $0$ unless we think it’s literally impossible.
We could fix this with some more complicated prior. What kind of properties would we want from such a prior?
- Ideally it would be a function of two values $B_{H,T}$, where $H$ and $T$ are the number of heads and tails respectively.
- As the number of trials tends to infinity, it should assign almost all of the probability density around $p={H \over H+T}$.
- If we have a prior of $B_{H_0,T_0}$, and we see $H$ heads and $T$ tails, our posterior would be $B_{H_0 + H, T_0 + T}$.
As it turns out, there is a distribution called the Beta Distribution which satisfies all of these. Usually written $\textrm{Beta}(H, T)$, though it’s important to remember, that this is a distribution of possible probability values, i.e. a function $[0,1]\to\mathbb{R}_{\geq 0}$. It’s the unique distribution which has all the nice properties you’d want for a binomial likelihood function (called a “conjugage prior” to the likelihood). Other likelihoods have different conjugate priors. To pick out a prior that applies for your domain, you can either start with some existing data, or play around with an interactive tool until you have a distribution that matches your best guess.
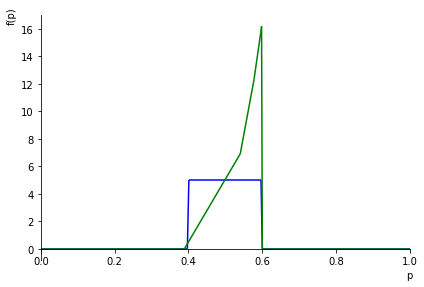
A good prior to start out with if you are going to be able to collect a bunch of data is an uninformative prior like the uniform $\textrm{Beta}(1, 1)$. In our example above, if we’d started out with an uninformative prior:
from sympy.stats import Beta, density
alpha_0, beta_0 = 1, 1
prior = density(Beta('prior', alpha_0, beta_0))(p)
posterior = density(Beta('posterior', alpha_0+15, beta_0+5))(p)
display(posterior)
p1 = plot(prior, xlim=[0,1], ylim=[0, 5], show=False, line_color='b')
p2 = plot(posterior, show=False, line_color='g')
p1.append(p2[0])
p1.show()
$\displaystyle \frac{p^{15} \left(1 - p\right)^{5}}{\operatorname{B}\left(16, 6\right)}$
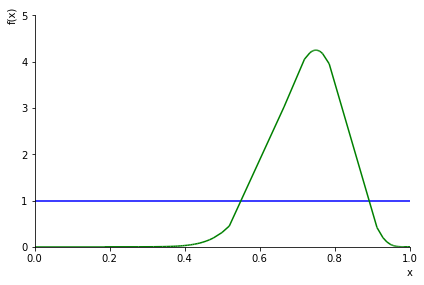
We can also do the update “manually” by integrating as above, and we should get a similar graph:
p, N = symbols("p N")
likelihood = sympy.binomial(20, 15) * p** 15 * (1-p)**5
P_D = integrate(prior * likelihood_D, (p, 0, 1))
p1 = plot(prior, xlim=[0,1], ylim=[0, 5], show=False, line_color='b')
p2 = plot(likelihood * prior / P_D, show=False, line_color='g')
p1.append(p2[0])
p1.show()